循環論法について
高校数学において、しばしば以下のパラドックス (循環論法) が話題になる。
- 小学校で、円周の長さ( $2\pi r$ )や円の面積( $\pi r^2$ )の公式を習う。というか仮定する。
- 1.の仮定を使って弧度法を定義し、また $\sin\theta$ や $\cos\theta$ を定義する。
- 1.の仮定を使って $\theta \rightarrow 0$ における極限値 $\sin\theta / \theta \rightarrow 1$ を導出する。
- 3.の結果と $\sin$ の加法定理を使って $\sin’\theta = \cos\theta$ の微分公式を導出する。
- 4.の結果を使って扇形の弧長 $\int _0^1 \sqrt{1+(y’)^2} dx$ を計算すると、 $\pi/2$ が得られる。
- 4.の結果を使って扇形の面積 $\int _0^1 \sqrt{1-x^2} dx$ を計算すると、 $\pi/4$ が得られる。
- 5.と6.の結果の相似を考えることで、1.の公式が導出される。
2-7.の計算は全て1.の仮定に依存している。 つまり1.の仮定を使って再び1.を導出しただけなので、この結果から1.の仮定を正当化することはできない。 例えると、 $1=2$ を仮定して $1=2$ を導いたところで $1=2$ が正当化されないのと同じことだ。 それゆえ1-7.の議論は循環論法とされる。
この循環論法に関連する話題として、3.の極限値の導出にもしばしば不備が指摘される。 論点は $ \sin\theta < \theta < \tan\theta $ という不等式で、これを円周の $2\pi r$ の式だけで示すのはかなり難しい(不可能ではない)。 面積の $\pi r^2$ の式を併用すれば簡単に示せるが、循環論法の循環っぷりが一層悪化する。
これらの課題に対し、本稿では高校数学の範囲で、上述の諸結果を見通し良く導出する方法を提示する。
議論の流れ
以下2つの汎用的な公式を用いる。 これらは円の話題と無関係に成り立つ。
- 一般の弧長公式 $\int _0^a \sqrt{1+(y’)^2} dx$
- 一般の面積公式 $\int _0^a y dx$
まず単位円 $x^2+y^2=1$ に一般の弧長公式を適用し、逆関数微分して $\sin’\theta = \cos\theta$ を示す。 そこに $\theta = 0$ を代入し、極限値 $\sin\theta / \theta \rightarrow 1$ を得る。
そして単位円に一般の面積公式を適用し、弧長が扇形の面積の倍になることを示す。 この関係式から $2\pi r$ と $\pi r^2$ の公式が導びかれる。
扇形の弧長
単位円の扇形の弧長を、下図のように $L(a)$ と定める。
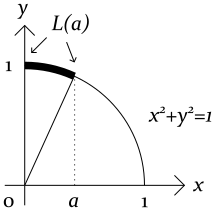
弧長 $L(a)$ は次の積分で求まる。
\[\begin{align} L(a) = \int _0^a \sqrt{1+(y')^2} dx \end{align}\]ここに $y=\sqrt{1-x^2}$ を微分した $y’=-x/\sqrt{1-x^2}$ を代入することで、次式を得る。
\[\begin{align} L(a) = \int _0^a \frac{dx}{\sqrt{1-x^2}} \end{align}\]三角関数
※ この結果は以降の節で使わない。
関数 $L(a)$ を $a$ で微分して逆数を取ると、次の式が得られる。
\[\begin{align} \frac{da}{dL} = \sqrt{1-a^2} \end{align}\]また $L(a)=\theta$ を $a$ について解いた式を $a = \sin\theta$ と書く。 これらを上式に代入することで次式を得る。
\[\begin{align} \frac{d}{d\theta} \sin\theta = \sqrt{1-\sin^2\theta} \end{align}\]右辺を $\cos\theta$ と書くことで、三角関数の微分公式 $\sin’\theta = \cos\theta$ を得る。 また $\theta = 0$ での微分係数を考えると
\[\begin{align} \lim_{h\rightarrow +0} \frac{\sin(0+h)-\sin(0)}{h} &= \sqrt{1-\sin^2(0)} \\ \lim_{h\rightarrow +0} \frac{\sin(h)}{h} &= 1 \end{align}\]$h\rightarrow -0$ の極限については、 $\sin(-\theta) = -\sin\theta$ と定義域を拡張することで上式同様 $1$ に収束する。 これらをまとめると次式の極限値が得られる。
\[\begin{align} \lim_{\theta\rightarrow 0} \frac{\sin(\theta)}{\theta} = 1 \end{align}\]円周と面積の比
単位円の第一象限(90度の扇形)の面積 $S$ は以下で与えられる。
\[\begin{align} S = \int _0^1 \sqrt{1-x^2}dx \end{align}\]これを $y=\sqrt{1-x^2}$ で置換積分する。 $dy/dx = -x/y$ に注意すると
\[\begin{align} S &= \int _1^0 y \left(-\frac{y}{x}\right) dy \\ &= \int _0^1 \left(\frac{y}{x}\right)^2 x dy \\ &= \int _0^1 \left(\frac{y^2}{1-y^2}\right) \sqrt{1-y^2} dy \\ &= \int _0^1 \left(-1+\frac{1}{1-y^2}\right) \sqrt{1-y^2} dy \\ &= -S + L(1) \end{align}\]よって $2S=L(1)$ が成り立つ。 さらに方程式 $x^2+y^2=1$ の $x$ と $y$ の反転対称性から、単位円の円周の長さは $8S$ で面積は $4S$ になることが分かる。
円周率
円周率 $\pi$ を単位円の円周の半分の長さと定義する。 前節の結果から
\[\begin{align} \pi = 4\int _0^1 \sqrt{1-x^2}dx \end{align}\]を得る。 また単位円の面積が $\pi$ になることが分かる。 さらに $L(1)$ と $S$ を求める積分の式に対し、 $rx=X$ と $ry=Y$ の置換を行うことで、半径 $r$ の円周の長さ $2\pi r$ と面積 $\pi r^2$ が得られる。
まとめ
ここまでの話をまとめる。
- 前提のツールとして、一般の弧長公式と面積公式を仮定した。これらは円と無関係に成り立つ公式。
- 三角関数の絡んだ公式は、単位円に一般の弧長公式を適用するだけで得られた。
- $2\pi r$ と $\pi r^2$ の公式は、単位円の $2S=L(1)$ という性質から導出した。
- (補足) もし $ \sin’theta = \cos\theta$ の公式を使ってよければ、 $\pi r^2$ の公式の導出はさらに簡単になる。
本稿からうまく排除できたイヤな議論をまとめる。
- $2\pi r$ と $\pi r^2$ から出発し、再び $2\pi r$ と $\pi r^2$ に戻ってくる循環論法を解消した。
- $2\pi r$ と $\pi r^2$ と三角関数の諸公式の依存関係を解消し、独立した議論にした。
- $\sin\theta/\theta$ の極限を求める際の、弧長と線分の長さの不等式評価を排除した。
- $\sin\theta/\theta$ の極限を求める際の、扇形と三角形の面積の (図を用いた) 不等式評価を排除した。